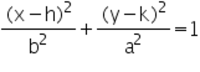ภาคตัดกรวย conic section

วันพุธที่ 21 มิถุนายน พ.ศ. 2560

ความรู้ทั่วไปเกี่ยวกับภาคตัดกรวย

ภาคตัดกรวย (conic section หรือ conic)

ในทางคณิตศาสตร์ หมายถึง เส้นโค้งที่ได้จากการตัดพื้นผิวกรวยกลม ด้วยระนาบแบน ภาคตัดกรวยนี้ถูกตั้งเป็นหัวข้อศึกษาตั้งแต่สมัย 200 ปีก่อนคริสต์ศักราชโดย อพอลโลเนียส แห่ง เพอร์กา ผู้ซึ่งศึกษาภาคตัดกรวยและค้นพบสมบัติหลายประการของภาคตัดกรวย ต่อมากรณีการศึกษาภาคตัดกรวยถูกนำไปใช้ประโยชน์หลายแบบ ได้แก่ ในปี พ.ศ. 2133 (ค.ศ. 1590) กาลิเลโอ กาลิเลอี พบว่าขีปนาวุธที่ยิงขึ้นไปในมุมที่กำหนดมีวิถีการเคลื่อนที่โค้งแบบพาราโบลา, ใน พ.ศ. 2152 (ค.ศ. 1609) โยฮันส์ เคปเลอร์ พบว่าวงโคจรของดาวเคราะห์รอบนอกเป็นรูปวงรี เป็นต้น ในกรณี ดีเจนเนอเรต ระนาบจะตัดผ่านจุดยอดของกรวย และได้ผลของการตัดเป็น จุด เส้นตรง หรือ เส้นตรงสองเส้นตัดกัน กรณีเหล่านี้ไม่ได้ถูกรวมไว้ในภาคตัดกรวย

ในเรขาคณิตเชิงภาพฉาย (projective geometry) นั้น ภาพฉายบนระนาบ ของภาคตัดกรวยแต่ละชนิดนั้นจะเหมือนกัน ขึ้นอยู่กับลักษณะการฉาย หรือที่เรียกว่า การแปลงเชิงภาพฉาย (projective transformation)

วงกลม

ในทางคณิตศาสตร์ ถือว่าวงกลมเป็นเส้นโค้งที่สมบูรณ์ เครื่องใช้ต่างๆ ของเรามักมีลักษณะเป็นวงกลม เช่น ขันตักน้ำ หน้าปัดนาฬิกา จานข้าว ถาด กระโถน เงินเหรียญ แก้วน้ำ ท่านลองตรวจดูของใช้รอบ ๆ กาย และทั่ว ๆ ไป จะเห็นว่าการใช้ของที่มีลักษณะเป็นวงกลมนั้นให้ความสะดวก มากที่สุด ลองนึกดูว่าถ้าล้อเกวียน ล้อจักรยานยนต์ ล้อรถยนต์ ไม่มีลักษณะ เป็นวงกลมแล้ว การเคลื่อนที่จะลำบากสักเพียงใด

วงรี

ยามค่ำคืนถ้าได้มีโอกาสสังเกตบนฟากฟ้าจะพบเห็นดาวที่สุกสว่างมีแสงเจิดจ้า ซึ่งได้แก่ดาวเคราะห์ และหากสังเกตต่อเนื่องไปหลาย ๆ วัน และอาจถึงหลายเดือนจะพบเห็นการเคลื่อนที่ผ่านกลุ่มดาวฤกษ์ ในทางดาราศาสตร์ พบว่าทางเดินของโลกและดาวเคราะห์ต่าง ๆ ที่เดินรอบดวงอาทิตย์ต่างก็ล้วนมีเส้นทางเป็นรูปวงรี โดยมีดวงอาทิตย์อยู่ที่จุดโฟกัสของวงรีแต่ละวง ดวงจันทร์ซึ่งเป็นดาวบริวารของดาวเคราะห์ก็เดิน ทางรอบดาวเคราะห์เป็นวงรี แม้ดาวเทียมที่มนุษย์ประดิษฐ์ขึ้นก็หมุนรอบโลก เป็นวงรี

กฎข้อที่ 1 ของเคปเลอร์ :
ดาวเคราะห์โคจรรอบดวงอาทิตย์เป็นวงรี โดยมีดวงอาทิตย์อยู่ที่โฟกัสจุดหนึ่ง

นักวิทยาศาสตร์ ยังได้พบว่าแม้แต่ในปรมาณูของธาตุต่าง ๆ เช่น อิเล็กตรอนก็เดินทางเป็นวงรีรอบนิวเคลียสของปรมาณูนั้น ๆ เราอาจนำเส้นโค้งแบบวงรีไปออกแบบเป็นเครื่องใช้ก็ได้ เช่น จานเปล ถังเปล เป็นต้น เราจะสังเกตว่ารถบรรทุกน้ำมันมักจะมีตัวถัง เป็นรูปทรงกระบอกซึ่งมีหน้าตัดเป็นรูปวงรี สนามกีฬาที่มีลู่แข่งขันกันก็มีลักษณะ เกือบเป็นวงรี

อิเล็กตรอน ทางเดินของโลกและดวงดาวต่างๆ

ถังเปล จานเปล

พาราโบลา

เทคโนโลยีการสื่อสารดาวเทียมประกอบด้วยจานรับสัญญาณ ตัวจานรับสัญญาณมีผิวโค้ง เพื่อรับสัญญาณที่ส่งตรงมาจากดาวเทียม และสะท้อนรวมกันที่จุดรับสัญญาณ เพื่อให้มีสัญญาณที่แรงขึ้น น้ำพุที่มนุษย์ประดิษฐ์ขึ้น เป็นเส้นโค้งพาราโบลา หรือเมื่อเราใช้ไฟฉายส่องเดินทาง สังเกตว่ามีกระจกสะท้อนแสงเพื่อรวมลำแสงให้พุ่งเป็นลำตรง โดยหลักการตามกฎการสะท้อนของแสง มุมตกกระทบย่อมเท่ากับมุมสะท้อน จุดที่รวมกันบนผิวระนาบโค้งนี้เรียกว่าจุดโฟกัส ผิวโค้งที่ทำให้มุมตกกระทบและสะท้อนมารวมกันที่จุดโฟกัส เรียกว่า ผิวโค้งพาราโบลา

จานรับสัญญาณ น้ำพุ

ไฮเปอร์โบลา

ภาคตัดกรวยนั้นได้มีความสำคัญต่อดาราศาสตร์ โดย วงโคจรของวัตถุสองชิ้นซึ่งมีแรงดึงดูดกระทำต่อกัน ตามกฏของนิวตัน นั้นจะมีรูปร่างเป็นภาคตัดกรวย หากจุดศูนย์กลางมวล (center of mass) ร่วมของทั้งสองวัตถุนั้นอยู่นิ่ง หากทั้งสองนั้นถูกดึงดูดอยู่ด้วยกัน ทางเดินของทั้งสองนั้นจะเป็นรูปวงรี หากวัตถุทั้งสองวิ่งออกจากกัน ทางเดินจะเป็นรูปพาราโบลา หรือ ไฮเปอร์โบลา

ลักษณะที่พบ

Flashlight Hyperbola Flashlight Parabola

หลังคาเป็นโค้งไฮเพอร์โบลา ไฮเพอร์โบลา

เส้นโค้งและผิวโค้งทางคณิตศาสตร์ยังมีอีกมาก และเป็นศาสตร์ที่สามารถนำมาใช้ในการออกแบบผลิตภัณฑ์ต่าง ๆ ได้มากมาย ลองค้นหาจากเอกสารต่าง ๆ ดูว่า เส้นโค้งทางคณิตศาสตร์ที่น่าสนใจเหล่านี้มีลักษณะอย่างไร cycloid, cardioid Ephicycloid Hypocycloid spiral ฯลฯ

ประโยชน์ของเส้นโค้งหรือผิวโค้งจึงมีมากมายและเกี่ยวข้องกับชีวิตประจำวันอย่างมาก เช่น ขณะขับรถไปในท้องถนน ถ้าวิศวกรออกแบบถนนให้มีส่วนโค้งของผิวถนนขณะขึ้นสะพาน และลงระนาบพอดี

สามารถค้นคว้าเนื้อหาเพิ่มเติมได้ที่
ติวฟรี.คอม

อ้างอิง
เกษรา จันทรฑีโร : หมวดคณิตศาสตร์ โรงเรียนสตรีวิทยา 2

กราฟและสมการของภาคตัดกรวย

กราฟและสมการของภาคตัดกรวยแต่ละชนิด โดยอาศัยหลักการเลื่อนกราฟ ได้ดังตารางต่อไปนี้

ภาคตัดกรวย	กราฟ	สมการรูปแบบมาตรฐานและข้อเท็จจริงที่สำคัญ
วงกลม		สมการ จุดศูนย์กลาง (h, k) รัศมียาว r หน่วย
วงรี		สมการ แกนเอกอยู่ในแนวนอน จุดศูนย์กลาง (h, k) จุดยอด (h-a, k), (h+a, k) โฟกัส (h-c, k), (h+c, k); c²= a² - b² แกนเอกยาว 2a หน่วย แกนโทยาว 2b หน่วย
วงรี		สมการ แกนเอกอยู่ในแนวตั้ง จุดศูนย์กลาง (h, k) จุดยอด (h, k-a), (h, k+a) โฟกัส (h, k-c), (h, k+c); c²= a² - b² แกนเอกยาว 2a หน่วย แกนโทยาว 2b หน่วย
พาราโบลา		สมการ แกนสมมาตรอยู่ในแนวตั้ง จุดยอด (h, k) โฟกัส (h, k+p) P > 0 เส้นโค้งหงายขึ้น P < 0 เส้นโค้งคว่ำลง ไดเรกตริกซ์ y = k – p
พาราโบลา		สมการ แกนสมมาตรอยู่ในแนวตั้ง จุดยอด (h, k) โฟกัส (h+p, k) P > 0 เส้นโค้งเปิดด้านขวา P < 0 เส้นโค้งเปิดด้านซ้าย ไดเรกตริกซ์ x = h – p
ไฮเพอร์โบลา		สมการ แกนตามขวางอยู่ในแนวนอน จุดศูนย์กลาง (h, k) จุดยอด (h-a, k), (h+a, k) โฟกัส (h-c, k), (h+c, k); c²= a² + b² แกนตามขวางยาว 2a หน่วย แกนสังยุคยาว 2b หน่วย
		สมการ แกนเอกอยู่ในแนวตั้ง จุดศูนย์กลาง (h, k) จุดยอด (h, k-a), (h, k+a) โฟกัส (h, k-c), (h, k+c); c²= a² + b² แกนตามขวางยาว 2a หน่วย แกนสังยุคยาว 2b หน่วย

สมการทั่วไปของภาคตัดกรวย

กราฟของสมการ เมื่อ A และ C ไม่เป็นศูนย์พร้อมกันเป็นภาคตัดกรวยหรือภาคตัดกรวยลดรูป ในกรณีที่ไม่ใช่ภาคตัดกรวยลดรูป กราฟของสมการเป็น

1. วงกลม ถ้า A = C

2. วงรี ถ้า AC > 0

3. พาราโบลา ถ้า AC = 0

4. ไฮเพอร์โบลา ถ้า AC < 0

สามารถค้นคว้าเนื้อหาเพิ่มเติมได้ที่
http://www.kr.ac.th/ebook/pasit/b4.htm
ติวฟรี.คอม

การพิจารณากราฟ

สามารถค้นคว้าเนื้อหาเพิ่มเติมได้ที่

ติวเตอร์ คณิต ฟิสิกส์.คอม

วันอังคารที่ 20 มิถุนายน พ.ศ. 2560

ภาคตัดกรวย

2.1. วงกลม (circle)

สมการวงกลม

วงกลม คือเซตของจุดทุกจุดซึ่งห่างจากจุดคงที่จุดหนึ่งเป็นระยะทางคงตัว จุดคงที่ เรียกว่า จุดศูนย์กลาง ส่วนระยะคงที่เรียกว่า รัศมี

นิยามของสมการวงกลมคือ

วงกลม (circle) คือเซตของจุดทั้งหมดในระนาบที่ห่างจากจุดๆหนึ่งตรึงอยู่กับที่เป็นระยะทางคงตัว จุดที่ตรึงอยู่กับที่นี้เรียกว่า จุดศูนย์กลาง (center) ของวงกลม และระยะทางคงตัวดังกล่าวเรียกว่า รัศมี (radius) ของวงกลม

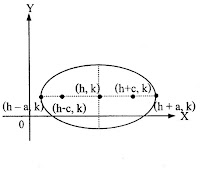
รูปที่ 1: สมการวงกลม

จุด C(h,k) เป็นจุดคงที่ เรียกว่า จุดศูนย์กลาง

|CP| = ระยะทางคงที่ เรียกว่ารัศมี

รูปแบบของสมการวงกลม

รูปที่ 2: รูปแบบของสมการวงกลม

ข้อสังเกตุ

1. ถ้า D² + E² – 4F = 0 กราฟที่ได้จะเป็นจุดวงกลม

2. ถ้า D² + E² – 4F > 0 กราฟที่ได้จึงเป็นวงกลม

3. ถ้า D² + E² – 4F < 0 จะไม่เกิดกราฟในระบบจำนวนจริง

ข้อสำคัญ

ในเรื่องวงกลม ถ้าต้องการหาสมการวงกลม จะต้องทราบ

1. จุดศูนย์กลาง

2. รัศมี

การหาจุดศูนย์กลางของวงกลม

การหาจุดศูนย์กลางของวงกลม จะหาได้ด้วยวิธีดังต่อไปนี้

1. โจทย์กำหนดมาให้โดยตรง เช่นให้จุดศูนย์กลางคือ C(h,k)

2. โจทย์กำหนดมาให้ทางอ้อม เช่นจุดที่เส้นตรงตัดกัน

3. โจทย์หำหนดมาให้ โดยมีความสัมพันธ์กับกราฟอื่นๆ

การหาความยาวรัศมี

การหาความยาวรัศมี จะหาได้ด้วยวิธีดังต่อไปนี้

1. โจทย์กำหนดมาให้โดยตรง (2¶r)

2. โจทย์กำหนดมาให้ทางอ้อม เช่นความยาวระหว่างจุดสองจุด หาได้จากสูตร

3. โจทย์กำหนดจุดศูนย์กลาง (h, k) และเส้นสัมผัส Ax + By + C = 0 เราจะหาทั้งเส้นผ่านศูนย์กลางและรัศมีได้จากสูตรต่อไปนี้

ความยาวของเส้นสัมผัส

ให้ |PQ| เป็นความยาวของเส้นสัมผัสที่ลากจากจุด P มาสัมผัสวงกลมที่จุด

1. ถ้าสมการวงกลมคือ x² + y² = r² แล้ว

|PQ| -

ดังรูป

2. ถ้าสมการวงกลมคือ (x-h)² + (y-k)² = r² แล้ว

|PQ|-

ดังรูป

3. ถ้าสมการวงกลมคือ x² + y² + Dx + Ey + F = 0 แล้ว

|PQ| =

ดังรูป

ตัวอย่างที่ 1

จงเขียนกราฟของสมการ (x + 2)² + (y – 3)² = 16

วิธีทำ กราฟของสมการที่กำหนดให้เป็นวงกลม ในการเขียนกราฟ จะต้องทราบตำแหน่งของจุดศูนย์กลางและความยาวของรัศมีของวงกลม ซึ่งหาได้โดยการเทียบสมการที่กำหนดให้กับรูปแบบมาตรฐานของสมการวงกลม จะพบว่า h = -2, k = 3 และ r – 4 ดังนั้น วงกลมมีจุดศูนย์กลางอยู่ที่ (-2, 3) และรัศมียาว 4 หน่วย การเขียนวงกลมขั้นแรก ลงจุดศูนย์กลางที่จุด (-2, 3) และเนื่องจากรัศมีของวงกลมยาว 4 หน่วย ลงจุดอีก 4 จุดห่างไปจากจุดศูนย์กลางไปทางด้านซ้าย ทางด้านขวา ทางด้านล่าง และทางด้านบน 4 หน่วย แล้ววาดวงกลมผ่านจุด 4 จุดนี้จะได้วงกลมดังแสดงในรูป

2.2. พาราโบลา

นิยามของสมการพาราโบลา

พาราโบลา คือเซตของจุดบนพื้นระนาบซึ่งมีระยะห่างจากจุดคงที่ เท่ากับระยะที่ห่างจากเส้นคงที่

จุดคงที่ คือจุ ดโฟกัส (Focus)

เส้นตรงที่คงที่ คือ เส้นไดเรกตริกซ์ (Directrix)

เส้นลาตัสเลกตัม (Latus Rectum) คือ เส้นตรงที่ลากผ่านจุดโฟกัสและตั้งฉากกับแกนของรูป

แกนของรูปหรือแกนสมมาตร คือ เส้นตรงที่ลากผ่านจุดยอดและผ่านจุดโฟกัส

คอร์ดของพาราโบลา คือเส้นตรงที่ลากเชื่อมจุด 2 จุด ที่ต่างกันของพาราโบลาและคอร์ดที่ลากผ่านจุดโฟกัสเรียกว่า Focul ส่วนคอร์ดที่ลากผ่านจุดโฟกัสด้วย และตั้งฉากกับแกนของรูปด้วย เรียกว่า ลาตัสเรกตัม (Latus Recrum)

ข้อสังเกตุ

จากสมการ จะต้องมีตัวแปรใดตัวแปรหนึ่งอยู่ในรูปกำลังสอง และอีกตัวหนึ่งยกกำลังหนึ่ง และอยู่ที่เทอมที่บวกลบกัน กราฟที่ได้จึงจะเป็นกราฟพาราโบลา

รูปแบบของพาราโบลาที่มีจุดศูนย์กลางอยู่ที่จุด (0,0)

พาราโบลาซึ่งมีจุดยอดที่จุด (0,0) และแกนของรูปทับแกน y

พาราโบลาซึ่งมีจุดยอดที่จุด (0,0) และแกนของรูปทับแกน x

เราสามารถสรุปสมการพาราโบลาออกมาได้ดังนี้

โจทย์พาราโบลา

เรียงจากง่ายไปยากนะครับ ลองทำกันดูนะ

EX1: จงหาสมการของพาราโบลาที่มีจุดโฟกัส (0,3) และจุดยอด (0,0)

วิธีทำ จากโจทย์ที่กำหนดให้ เราสามารถวาดกราฟพาราโบลาได้ดังนี้

จากรูปเป็นพาราโบลาหงาย มีจุดยอดคือ (0,0) จุดโฟกัสคือ (0,3) และได้ค่า c=3

สมการพาราโบลาของกราฟนี้คือ x²=4cy แทนค่า c=3 ในสมการจะได้

x²=(4)(3)y

x²=12y

2.3. วงรี

นิยามสมการวงรี

วงรี (Ellipse) คือเซตของจุดทั้งหมดในระนาบซึ่งผลบวกของระยะทางจากจุดใดๆจุดหนึ่งในเซตไปยังจุดคงที่ 2 จุดมีค่าคงตัว

จากบทนิยามนี้ มีวิธีง่ายๆ ในการวาดรูปวงรี (ดูรูปที่ 2) วางกระดาษบนกระดานวาดรูปปักหมุด 2 ตัวที่จุดต่างกัน ใช้เป็นโฟกัสของวงรี ตัดเชือกเส้นหนึ่งยาวกว่าระยะทางระหว่างหมุดทั้งสอง ผูกปลายเชือกแต่ละข้างกับหมุด โดยใช้ดินสอรั้งเชื่อให้ตึงตลอดเวลา ขณะที่ค่อยๆ เคลื่อนดินสอรอบโฟกัส รอยดินสอที่เกิดขึ้นจะเป็นรูปวงรีเพราะผลบวกของระยะทางจากจุดปลายดินสอถึงโฟกัสทั้งสองเท่ากับความยาวของเชือกที่มีความยาวคงตัวเสมอ

ถ้าเชือกยาวกว่าระยะห่างระหว่างโฟกัสเพียงเล็กน้อย วงรีที่วาดได้จะมีรูปร่างเรียวยาว ดังเช่นในรูปที่ 3ก แต่ถ้าโฟกัสอยู่ใกล้กันเมื่อเปรียบเทียบกับความยาวของเชือก (เชือกยาวกว่าระยะห่างระหว่างโฟกัสมาก) วงรีที่วาดได้จะเกือบกลม ดังเช่นในรูปทางขวา ยิ่งถ้าจุดโฟกัสใกล้กันเท่าไหร่ ก็จะยิ่งกลมขึ้นๆ

ส่วนประกอบของวงรี

F, F’ เป็นจุดคงที่ เรียกว่าจุดโฟกัส (Focus)

V, V’ เป็นเส้นตรงที่ผ่านจุดโฟกัส และมีจุดปลายทั้งสองเป็นจุดยอด เรียกว่า แกนนอก

B, B’ เป็นเส้นตรงที่ผ่านจุดศูนย์กลางและตั้งฉากกับแกนเอก โดยมีจุดปลายทั้งสองอยู่บนวงรี เรียกว่า แกนโท

m₁m₂, m₁‘m₂‘ เป็นเส้นตรงที่ผ่านจุดโฟกัส และตั้งฉากกันแกนของรูป เรียกว่าเส้นลาตัสเรกตัม

วงรีที่มีจุดศูนย์กลางอยู่ที่จุด (0,0)

วงรีที่มีจุดศูนย์กลางอยู่ที่จุดกำเนิดและแกนเอกอยู่บนพิกัด

สรุปสมการวงรี

ตัวอย่างโจทย์สมการวงรี

EX1: วงรีรูปหนึ่งมีสมการเป็น = 1

จงหาโฟกัส จุดยอด ความยาวของแกนเอกและแกนโท และเขียนวงรี

วิธีทำ จากสมการ = 1 เมื่อเทียบกับรูปแบบมาตรฐาน = 1

จะได้ว่า a² = 16, b² = 4 นั่นคือ a = 4, b = 2

เนื่องจากพจน์ a² เป็นตัวส่วนของพจน์ x²

แกนเอกจึงอยู่บนแกน X ถ้าให้จุด (-c, 0) และ (c, 0) เมื่อ c > 0 เป็นโฟกัส

จะได้ว่า c² = a² – b² = 16 – 4 = 12 นั่นคือ c =

ดังนั้น สรุปได้ว่า

โฟกัสของวงรี คือ (-, 0) และ (, 0)

จุดยอด คือ (-4, 0) และ (4, 0)

แกนเอกมีความยาว 8 หน่วย

แกนโทมีความยาว 4 หน่วย

กราฟวงรีแสดงได้ดังรูปนี้

2.4. ไฮเพอร์โบลา

นิยามของสมการไฮเพอร์โบลา

ไฮเพอร์โบลา (Hyperbola) คือเซตของจุดทั้งหมดในระนาบซึ่งผลต่างของระยะทางจากจุดใดๆไปยังจุด F1 และ F2 ที่ตรึงอยู่กับที่มีค่าคงตัว โดยค่าคงตัวน้อยกว่าระยะห่างระหว่างจุดคงที่ที่ตรึงอยู่กับที่ทั้งสอง จุด F1 และ F2 ดังกล่าวนี้เรียกว่า โฟกัส (Focus) ของไฮเพอร์โบลา

ให้ระยะทางจากจุด F1 และ F2 ไปยังเส้นกราฟมีค่าเท่ากับ r1=F1 และ r2=F2 และระยะทางระหว่างจุด F และจุด F2 มีค่าเท่ากับ 2c หรือเรียกอีกอย่างว่าค่า k ซึ่งค่า k นี้จะมีค่าเป็นบวกเสมอ

r2-r1 = k

ถ้าจุด P ซึ่งอยู่บนเส้นกราฟด้านซ้ายมืออยู่บนแกน x แล้ว

k = (c+a) – (c-a) = 2a

ดังนั้นเราสามารถคำนวณค่า k=2a ได้ หรือนั่นก็คือระยะทางระหว่างจุดยอดของกราฟไฮเพอร์โบลาทั้งสอง ข้อสังเกตุคือเส้นกราฟพาราโบลาที่เกิดจาดจุดโฟกัส F1 จะมีเส้นกราฟที่เกิดจาด F2 สะท้อนเหมือนกันอยู่ในฝั่งตรงข้ามเสมอ

สมการไฮเพอร์โบลา

รูปแบบของสมการไฮเพอร์โบลาจะแบ่งออกตามรูปกราฟสมการสองแบบ คือไฮเพอร์โบลาแบบตะแคง (ซ้ายขวา) และไฮเพอร์โบลาแบบตั้ง (บนล่าง) โดยทั้งสองรูปแบบมีสมการดังนี้

ไฮเพอร์โบลาตะแคง

ไฮเพอร์โบลาตั้ง

สมการไฮเพอร์โบลาคือถ้าจุดศูนย์กลางของสมการ c อยู่ที่จุด (0,0) เราจะได้สมการไฮเพอร์โบลาที่จุดกำเนิดดังนี้

สังเกตว่าหน้า x เป็นบวก ดังนั้นแกนตามขวางจึงวางตัวในแนวแกน x (a อยู่กับ x)แกนตามขวาง (แกนที่ลากตัดกึ่งกลางของกราฟ) มีความยาวเป็น 2a

แกนสังยุค มีความยาวเป็น 2b

ระยะโฟกัส มีความยาว

แกนสังยุค มีความยาวเป็น 2b

ระยะโฟกัส มีความยาว

ข้อสังเกตุ: a ไม่จำเป็นต้องยาวกว่า b เหมือนในสมการวงรี แต่ถ้า a=b จะได้สี่เหลี่ยมจัตุรัสอยู่ตรงกลาง จะเรียกว่าเป็น ไฮเพอร์โบลามุมฉาก (Rectangular Hyperbola)

โจทย์ไฮเพอร์โบลา

ตัวอย่างที่1: จงหาจุดศูนย์กลาง จุดโฟกัส จุดยอด ความยาวของแกนตามขวาง ความยาวแกนสังยุค ความยาวเส้นลาตัสเรกตัม ค่าเอ็คเซนตริกซิตี (e) และสมการเส้นกำกับของไฮเพอร์โบลาต่อไปนี้ พร้อมทั้งวาดกราฟ